The Method of Least Squares
Fitting a regression model by minimizing RSS
The Ideas in Code
Writing a function in R
We have been using functions that already exist in either the base installation of R or in another package, such as dplyr, ggplot2 or stat20data, but sometimes it can be useful to write our own functions.
Custom functions in R can be created with the function function() (quite meta) and assigned to an object. The arguments that we would like the function to take go inside the parentheses of function(). The things that we would like the function to do go inside {}.
Here is a representation of \(f(x) = (x+.5)^2\) in R, which we are saving into the object f. Once we run the following code, we’ll have access to f in our environment and can use it.
f(x = 1.5)[1] 4Nelder-Mead on a simple function
Here, we plot the function \(f(x)\) that we described above over the \(x\) values \([-1,1]\).
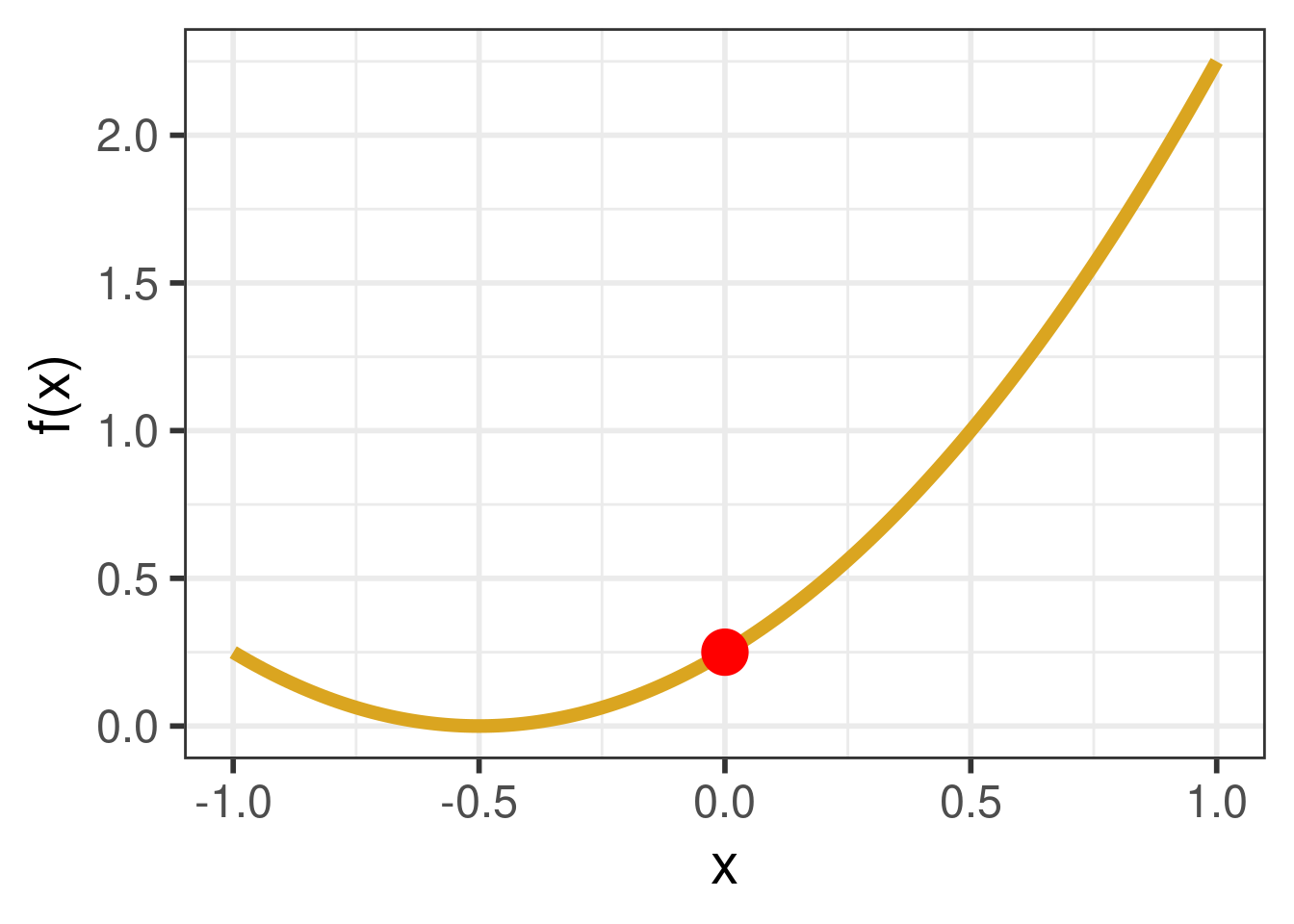
We can see that the minimum value of \(f(x)\) lies between \(-1\) and \(1\). Can we find the value of \(x\) that will give us this minimum using Nelder-Mead? We can try, using the optim() function!
optim()
There are two main arguments to modify:
The function to optimize is passed to
fn. In this case, the function we made is calledf.You provide a starting point for the algorithm with
par.- In this situation, we are trying to find the value of \(x\) to minimize \(f(x)\), so we will enter a number. We’ll start with \(x = .5\), but you can tinker around yourself and try something different. Depending on what you start with, you may come up with something different as a final answer, so feel free to try out different numbers!
- In a linear regression context, we are trying find the values of the coefficients \(b_0\) through \(b_p\) to minimize \(\hat{y}\), so we need to input a vector of starting values, one for each coefficient. This can be done using
c().
Nelder-Mead is a random algorithm; each time you run it you’ll get a (slightly) different answer. We therefore use set.seed() to make sure the same value is printed out for the purpose of publishing these notes.
set.seed(5)
optim(par = .5, fn = f)$par
[1] -0.4
$value
[1] 0.01
$counts
function gradient
12 NA
$convergence
[1] 0
$message
NULLYou don’t need to understand the entirety of the output given by optim()– just focus on the number under $par. This is the value of \(x\) that optim() thinks will give the minimum value of \(f(x)\) after. In truth, the correct value is \(-0.5\), so we didn’t fare too badly!