Causal Effects in Observational Studies

Natural experiments and matching

The Ideas in Code

We use the MatchIt package in R to conduct optimal matching using the Euclidean distance. The command matchit uses a formula argument much like lm to specify the treatment variable and the covariates on which to match. We also specify that we’re doing optimal matching and using a Euclidean distance.

library(MatchIt)
grad_matched <- matchit(cal_grad ~ GPA + years_exp + rec, method = 'optimal',
                        distance = 'euclidean',
                        data = grad_job)

Calling plot on objects created by matchit gives you diagnostics comparing the similarity of treated and control covariates before and after matching

plot(grad_matched, type = 'density')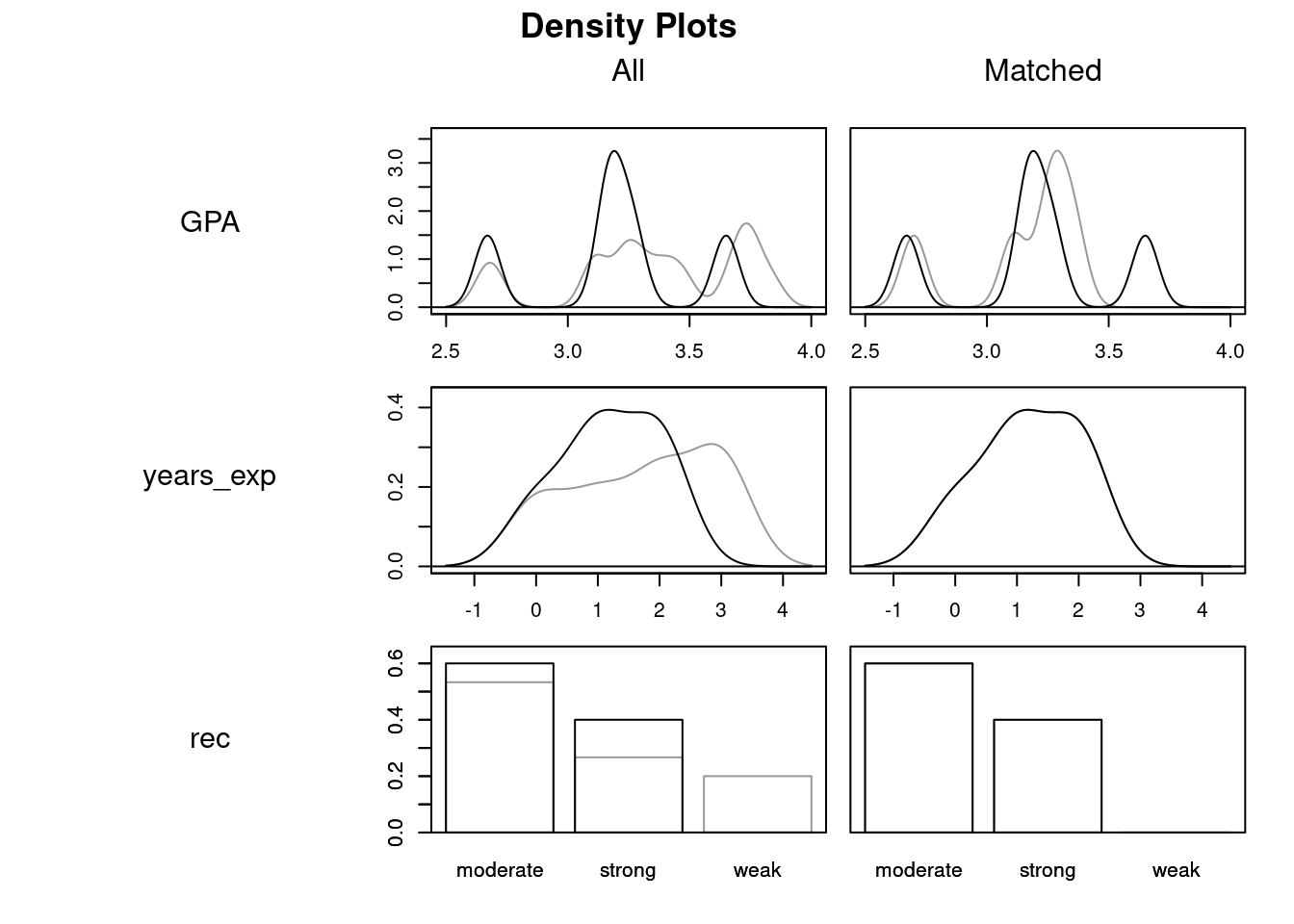

We can also pass matchit objects into the bal.test command and use the argument un = TRUE to create a Love plot with both pre- and post-matching covariate SMDs.

grad_matched |>
  bal.tab(s.d.denom = 'pooled', binary = 'std', un = TRUE) |>
  plot()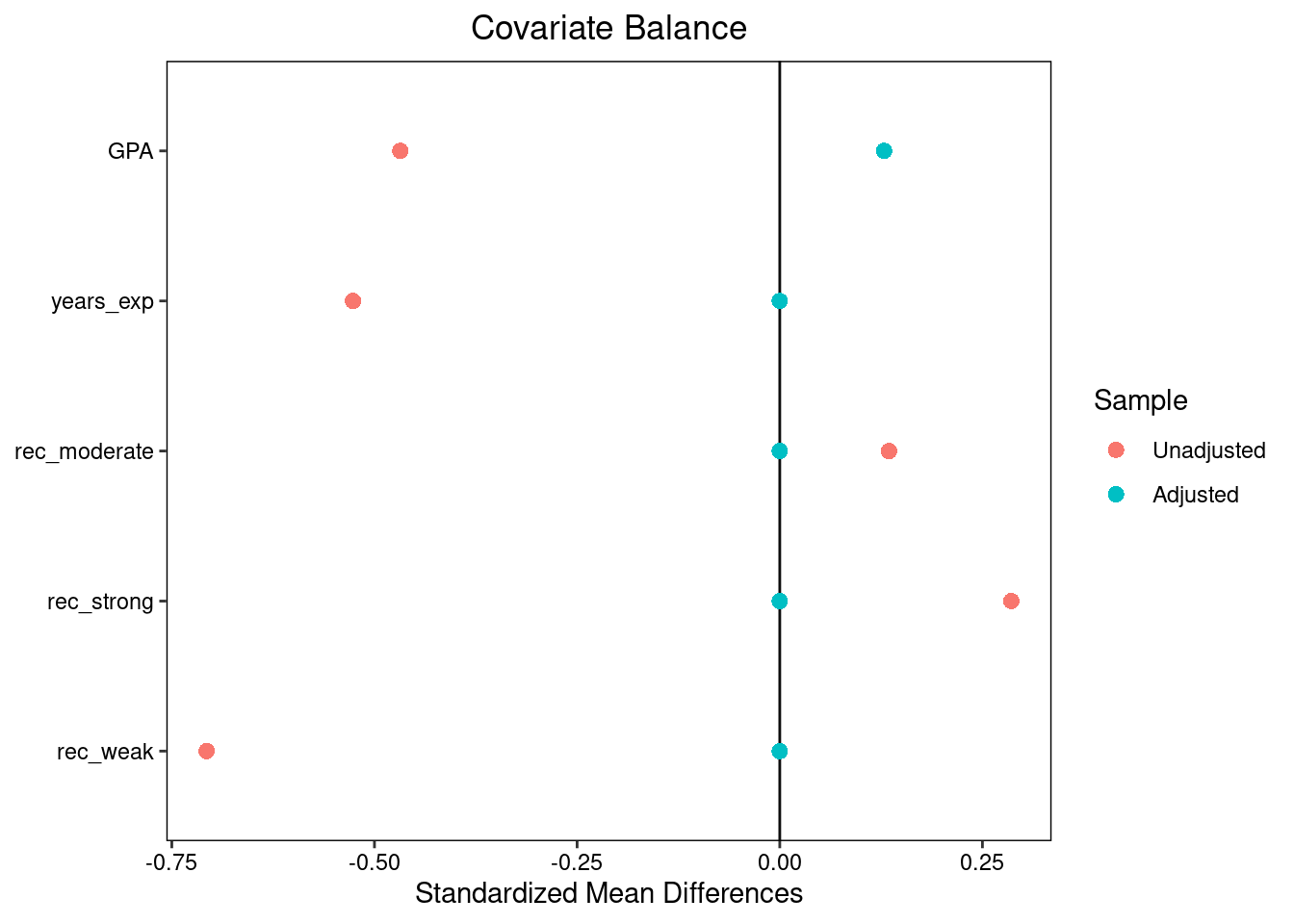

Since after matching our comparison groups closely resemble what we might have seen in a randomized experiment, we report the sample difference in means as our estimate of the average treatment effect and conduct a hypothesis test as we would have in a randomized trial where we were able to assign Berkeley graduation status at random. To use the data only from the matched individuals, rather than everyone in grad_job, we start with the output object from the matching step and pipe it to the match.data command to obtain the smaller data frame.

library(infer)
grad_matched |>
   match.data() |>
   specify(response = good_job,
          explanatory = cal_grad,
          success = "yes") |>
  calculate(stat = "diff in props", order = c("TRUE","FALSE"))

Response: good_job (factor)
Explanatory: cal_grad (factor)
# A tibble: 1 × 1
   stat
  <dbl>
1   0.4

We estimate that graduation from Cal increases the probability of obtaining a good job by 0.4.

Summary

We don’t need to give up on evaluating causal claims just because we are unable to assign treatments at random as in an experiment. In the best case, we can find natural experiments, or situations where nature or someone else assigns treatments essentially at random. Even if a natural experiment isn’t available, we can attempt to approximate one by finding similar individuals with different treatment status in the same data set by matching subjects on their covariates. When matched comparisons balance observe covariates well we can argue in favor of causal claims, although concerns about unobserved covariates (which are absent in randomized trials) remain.