Wrong By Design

STAT 20: Introduction to Probability and Statistics

Concept Questions

From your Lab Part 2:

Create a 95% confidence interval using the normal curve for the overall proportion of students who support the People’s Park Project without having been exposed to the information on page 14. Interpret the interval in the context of the problem in a clear sentence. Does your point estimate approximately match that reported in the Chancellor’s email?

Instead of constructing a confidence interval to learn about the parameter, we could assert the value of a parameter and see whether it is consistent with the data using a hypothesis test. Say you are interested in testing whether there is a clear majority opinion of support or opposition to the project.

What are the null and alternative hypotheses?

01:00

The null is the p = .5 and the alternative is that p != .5.

This brings up a good discussion of one- and two-tailed tests. When students share their answers, you can draw a picture of a null distribution on the board with the observed statistic as a vertical line and consider how the p-value calculation would change depending on the alternative hypothesis.

This also brings up a discussion of the link between hypothesis tests and confidence intervals. Below the picture of the null distribution on the board, you could draw a bootstrap distribution centered on the vertical line of the observed statistic. In the HT setting, you consider the location of the statistic relative to the null distribution. In making a decision with a CI, you consider the location of the parameter relative to the bootstrap distribution (or more generally, the sampling distribution of the statistic).

library(tidyverse)
library(infer)
library(stat20data)

ppk <- ppk |>
  mutate(support_before = Q18_words %in% c("Somewhat support", 
                                          "Strongly support",
                                          "Very strongly support"))

library(tidyverse)
library(infer)
library(stat20data)

ppk <- ppk |>
  mutate(support_before = Q18_words %in% c("Somewhat support", 
                                          "Strongly support",
                                          "Very strongly support"))
obs_stat <- ppk |>
  specify(response = support_before,
          success = "TRUE") |>
  calculate(stat = "prop")

library(tidyverse)
library(infer)
library(stat20data)

ppk <- ppk |>
  mutate(support_before = Q18_words %in% c("Somewhat support", 
                                          "Strongly support",
                                          "Very strongly support"))
obs_stat <- ppk |>
  specify(response = support_before,
          success = "TRUE") |>
  calculate(stat = "prop")
obs_stat

Response: support_before (factor)
# A tibble: 1 × 1
   stat
  <dbl>
1 0.339

null <- ppk |>
  specify(response = support_before,
          success = "TRUE") |>
  hypothesize(null = "point", p = .5) |>
  generate(reps = 500, type = "draw") |>
  calculate(stat = "prop")

null <- ppk |>
  specify(response = support_before,
          success = "TRUE") |>
  hypothesize(null = "point", p = .5) |>
  generate(reps = 500, type = "draw") |>
  calculate(stat = "prop")
null

Response: support_before (factor)
Null Hypothesis: point
# A tibble: 500 × 2
   replicate  stat
   <fct>     <dbl>
 1 1         0.507
 2 2         0.510
 3 3         0.483
 4 4         0.482
 5 5         0.491
 6 6         0.507
 7 7         0.505
 8 8         0.492
 9 9         0.508
10 10        0.502
# ℹ 490 more rows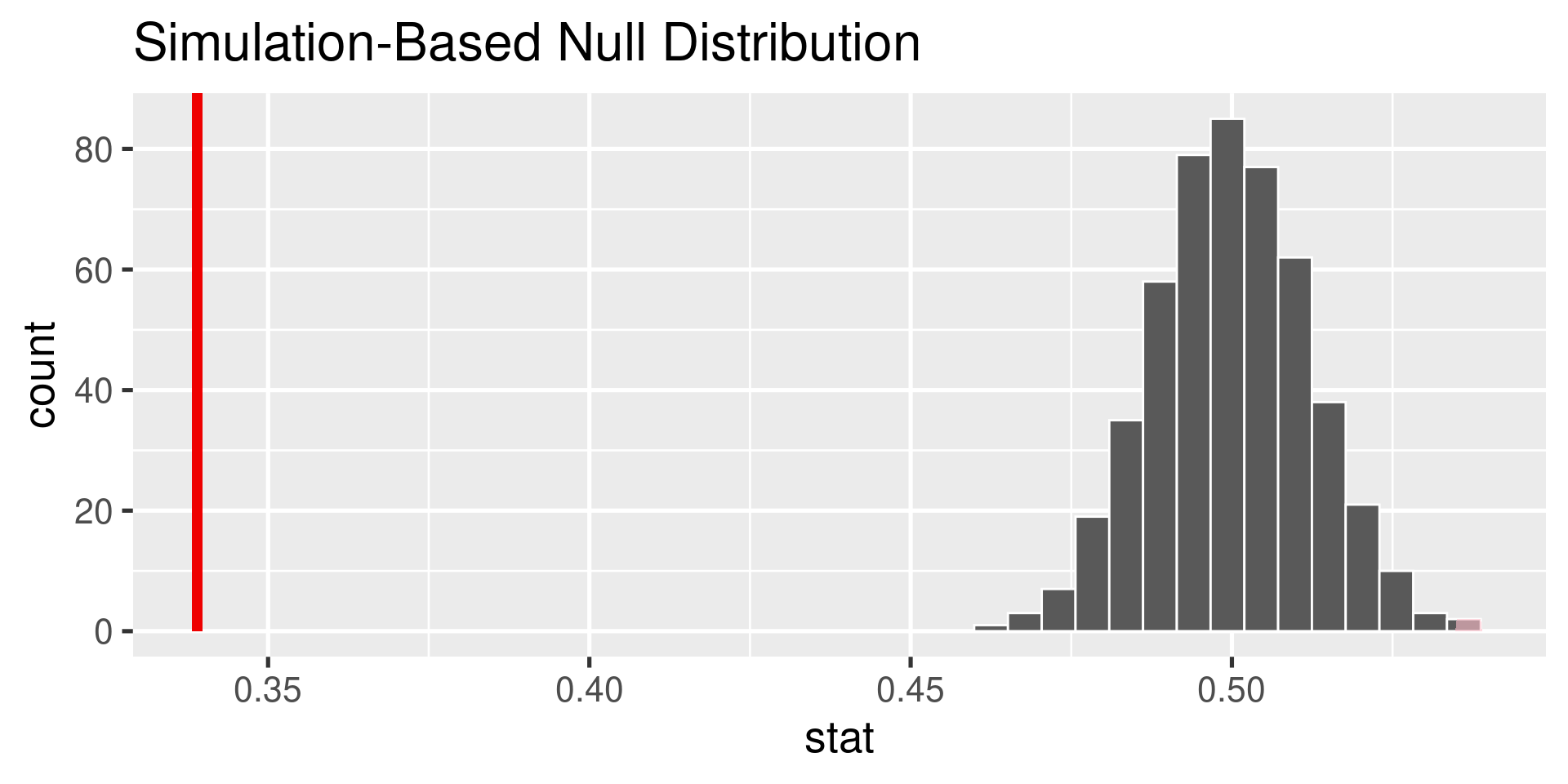

null <- ppk |>
  specify(response = support_before,
          success = "TRUE") |>
  hypothesize(null = "point", p = .5) |>
  generate(reps = 500, type = "draw") |>
  calculate(stat = "prop")
visualize(null) +
  shade_p_value(obs_stat, direction = "both")

What would a Type I error be in this context?

Answer: Concluding that there is a clear majority one way or another when in fact there is an even split.

01:00

What would a Type II error be in this context?

Answer: Concluding that there is an even split when in fact there is a clear majority.

After the previous question, students should get this quite easily.

One-question checkin (THIS HELPS US IMPROVE THE COURSE)